Network system dynamics

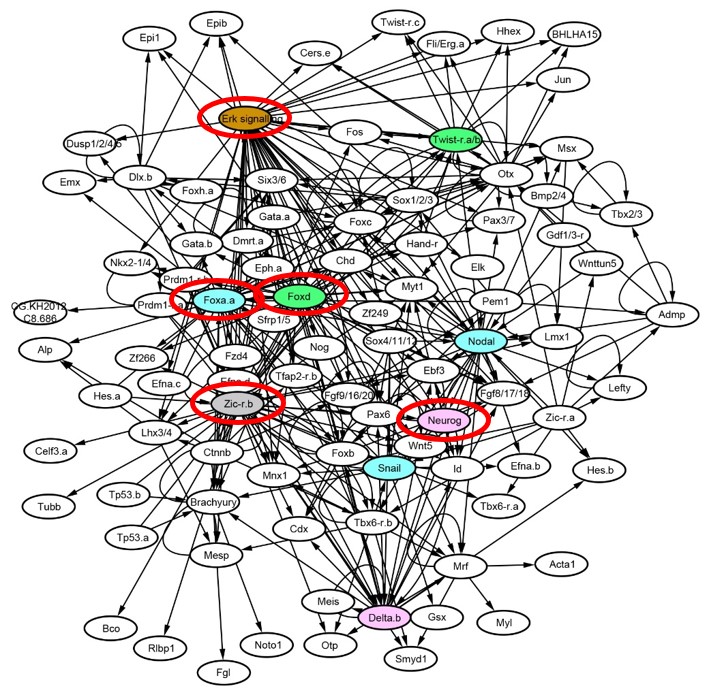
With the development of life science, it has become clear that various biological phenomena are dominated by networks in which biomolecules interact in a complex manner. It is believed that vital functions are born from the dynamics of these systems as a whole. We have independently developed several mathematical theories and structural theories that can determine important aspects of dynamics from only the information of the network, even if it is a complicated system. For example, according to the structural theory of linkage logic, some important components can be determined just from the structure of the control network, and all possible behaviors of the entire system can be reproduced simply by manipulating the behavior of those components. By applying this theory to a biological network of actual organisms and repeating theoretical prediction and experimental verification, we can understand the operating principle of the system.

Physical elucidation of intracellular structure

The function of eukaryotic cells is supported by structures such as organelles and cytoskeleton. These structures are composed of a large number of molecules that are self-organized and aggregated, and each of them has a characteristic morphology and behaves dynamically to carry out cell functions. The nature of the structure linked to this “shape” and “movement” is a problem that is difficult to reduce to the function of individual molecules and difficult to understand by conventional methods. We aim to understand this function by modeling the morphology and dynamics of biological structures using methods of statistical physics, soft matter physics, and complex system science.